Collision Detection - Xét Va Chạm Giữa Hình Tròn và Hình Tròn

Va chạm giữa hình tròn và hình tròn

Thuật toán

Mọi điểm nằm trên đường tròn cách đều tâm, nên việc kiểm tra va chạm giữa hai hình tròn sẽ được xác định dựa vào khoảng cách tâm giữa chúng.

Cho 2 đường tròn:

• C1 có bán kính r1 và tâm có toạ độ A(x1; y1).
• C2 có bán kính r2 và tâm có toạ độ B(x2; y2).

Để xác định khoảng cách giữa hai điểm, dựa vào công thức:

AB = √((x1 - x2)2 + (y1 - y2)2)

Phân tích

Hai đường tròn C1 và C2 rời nhau

Khi: AB > r1+ r2

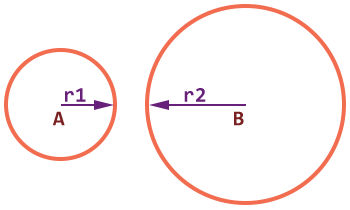
Hai đường tròn C1 và C2 lồng nhau

Khi: AB < r1 + r2

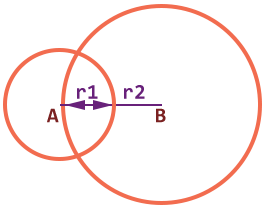
Ngoài ra còn trường hợp tiếp xúc: AB = r1 + r2

Code mẫu C++ xét sự tương quan giữa 2 hình tròn

struct Point
{
    double x;
    double y;

    Point(Point p)
    {
        x = p.x;
        y = p.y;
    }
};

struct Circle
{
    Point O;
    double r;

    Circle(Point _o, double _r) : Point(_o)
    {
        r = _r;
    }
};

double distance2(Point A, Point B)
{
    return (A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y);
}

bool checkCollision(Circle c1, Circle c2)
{
    return ((c1.r + c2.r) * (c1.r + c2.r) < distance2(c1.O, c2.O));
}

int main()
{
    Point p1(2.5, 6.6);
    Point p2(3.7, 7.3);

    Circle c1(p1, 2.5), c2(p2, 3.4);

    if(checkCollision(c1, c2))
	    cout << "AB";
    else
	    cout << "A   B";

    return 0;
}

Bài chung series

• Collision Detection - Xét Va Chạm Giữa Hình Tròn với Hình Tròn
• Collision Detection – Xét Va Chạm Giữa Hình Tròn Với Hình Chữ Nhật
• Collision Detection - Xét Va Chạm Giữa Hình Chữ Nhật Với Hình Chữ Nhật